مجموعه ها در ریاضیات — مفاهیم پایه

مجموعه ها و تعاریفی مانند اجتماع و اشتراک از بنیادی ترین مفاهیم در ریاضیات هستند و غالباً نقطه آغازی برای ریاضیات پایه و کاربردهای آن در بسیاری از علوم محسوب می شوند. مثلاً در رشته مدیریت در موارد بسیاری صحبت از مجموعه تولیدات یک کارخانه یا مجموعه کارگران یک کارگاه یا مجموعه تصمیم‌های ممکن برای مدیر یک واحد و نظایر آن به میان می‌آید.

مفهوم شهودی مجموعه

مفهوم ریاضی یک مجموعه با مفهوم شهودی (عادی یا روزمره) آن تفاوت دارد. یک مجموعه از نظر ریاضی هنگامی معین است که اشیای تشکیل دهنده آن کاملاً مشخص باشند.

به بیان دیگر باید برای هر شیء به دقت بتوان تعیین کرد که آن شیء به یک مجموعه تعلق دارد یا نه. برای مثال  مجموعه دانشحویان رشته مدیریت دانشگاه‌های ایران یک مجموعه ریاضی نیز به حساب می آید، زیرا به دقت می توان تک تک این افراد را مشخص کرد. اما دسته دانشجویان باهوش دانشگاه تهران در سال جاری یک مجموعه محسوب نمی‌شود. زیرا با هوش بودن یک صفت نسبی (غیر مطلق) است؛ یعنی دقیقاً نمی‌توان تعیین کرد که دانشجویی باهوش است یا خیر. در نتیجه افراد تشکیل دهنده این دسته معین نیستند.

بنابراین متوجه شدیم که مجموعه متشکل از همه اشیایی است که صفتی مشترک داشته باشند. بنابراین ابتدا یک ویژگی معمول برای دسته‌ای از اشیا مشخص می‌کنیم و سپس تمامی اشیایی که این ویژگی معمول را دارند جمع آوری کنیم.

بعنوان مثال، سعی کنید چیزهایی که می‌پوشید را برشمارید: کفش، جوراب، کلاه، پیراهن، شلوار، غیره. مطمئناً می‌توانید به حداقل صد نوع از این اشیا اشاره کنید. این دسته بعنوان مجموعه شناخته می شود. یک مثال دیگر انگشت های دست هستند. این مجموعه شامل انگشت‌ سبابه، انگشت اشاره، انگشت وسط، انگشت حلقه، و انگشت کوچک است. پس یک مجموعه شامل اشیایی به صورت یک دسته است که همه ی عضوها ویژگی مشترکی دارند.

با توجه به این‌که مجموعه یکی از دروس ریاضی نهم نیز به شمار می‌آید، برای آشنایی بیشتر با این درس، مطالعه مطلب زیر پیشنهاد می‌شود.

• تدریس فصل اول ریاضی نهم — راهنمای کامل + منابع رایگان

نماد

یک نماد ساده برای مجموعه‌ها وجود دارد. کافی است تمامی عضوهای مجموعه را پشت سر هم بنویسیم. بین آنها علامت کاما "," قرار دهیم و سپس در دو طرف این مجموعه علامت های آکولاد {  } بگذاریم. در صورتی که آخرین عضو یک مجموعه به صورت علامت سه نقطه (...) باشد، به این معنی است که اعضای این مجموعه بیش از آنهایی است که نوشته شده‌اند.

برخی از مجموعه‌ها نیز وجود دارند که اعضایشان محدود نیست و می توان بی‌شمار از اعضای آنها را شمرد. به چنین مجموعه‌هایی، مجموعه نامتناهی گفته می‌شود. بدیهی است که به مجموعه‌هایی که اعضای آنها قابل شمارش باشد، مجموعه متناهی گفته می‌شود.

می توان علامت سه نقطه (...) را در وسط یک مجموعه نیز استفاده نمود و بدین ترتیب از نوشتن اعضای اضافی و ایجاد یک فهرست بلند پرهیز کرد:

مثال: مجموعه حروف الفبای فارسی:

{الف، ب، پ، ...، و، ه، ی}

این مجموعه یک مجموعه متناهی است.

مجموعه های عددی

سوالی که در این مرحله ممکن است بریتان پیش بیاید این است که این مجموعه ها در ریاضیات به چه دردی می‌خورند؟ هنگامی که یک مجموعه را تعریف می‌کنیم، تنها چیزی که باید مشخص شود، خصوصیات مشترک آنهاست. در مورد اعداد نیز جر این نیست. در ادامه برخی مجموعه‌های اعداد را به همراه صفت مشترکی دارند، ارائه کرده‌ایم:

• مجموعه اعداد زوج: { … , 4 , 2 ,0 ,2- ,4- , …}
• مجموعه اعداد فرد: {… , 3 ,1 ,1- ,3- , …}
• مجموعه اعداد اول: {... ,17 ,13 ,11 ,7 ,5 ,3 ,2}
• مجموعه مضرب های مثبت عدد 3 کمتر از 10: {9 ,6 ,3}

مجموعه‌های عد بی شماری وجود دارند و می‌توانیم چندین مجموعه دیگر نیز معرفی کنیم. همچنین می‌توان مجموعه اعدادی تعریف کرد که هیچ ویژگی مشترکی با هم نداشته باشند و فقط در آن مجموعه معرفی شده باشند. برای مثال:

{2, 3, 6, 828, 3839, 8827}

{4, 5, 6, 10, 21}

{2, 949, 48282, 42882959, 119484203}

تمامی این ها مجموعه هایی هستند که به طور تصادفی با فشردن اعداد صفحه کلید به دست آمده‌اند.

چرا مجموعه ها مهم هستند؟

مجموعه ها ویژگی ابتدایی ریاضیات است. ممکن است به نظر بیاید که مجموعه‌ها فی نفسه بی‌اهمیت هستند؛ اما در موقعیت‌های مختف که از مجموعه‌ها استفاده می‌کنیم، می‌بینیم که آنها آجرهای سازنده ساختمان ریاضیات هستند.

ریاضیات می تواند به سرعت پیچیده شود. نمودار، تئوری، جبر مجرد، آنالیز اعداد حقیقی، آنالیز اعداد مختلط، جبر خطی، تئوری اعداد، و مواردی از این دست همگی شاخه‌های مختلف ریاضیات هستند؛ اما یک چیز وجود دارد که در همه آنها مشترک است و آن مجموعه‌ها هستند.

مجموعه جهانی

در ابتدای این نوشته از کلمه اشیا استفاده کردیم. مجموعه‌های جهانی را به این دلیل چنین نامگذاری کرده‌اند چون مجموعه‌ای است که شامل هر چیزی در جهان می‌شود. البته منظورمان از همه چیز، واقعاً همه چیز نیست؛ بلکه هر چیزی که به موضوع مجموعه مربوط باشد.

مثلا در مورد مجموعه‌های شامل اعداد صحیح، مجموعه‌ی جهانی می‌تواند شامل تمامی اعداد صحیح باشد. در واقع، هنگام کار با نظریه اعداد، منظور از مجموعه‌ جهانی همان مجموعه اعداد صحیح است، زیرا این مجموعه اعدادی است که مورد مطالعه قرار می‌گیرند.

            

اما در حساب دیفرانسیل و انتگرال که آنالیز اعداد حقیقی نیز نامیده می شود، منظور از مجموعه جهانی تقریباً برابر با اعداد حقیقی است. همچنین در مورد آنالیز اعداد مختلط، همان طور که احتمالاً حدس زده اید، منظور از  مجموعه جهانی، مجموعه  اعداد مختلط است.

نمادهای بیشتر

هنگامی که از مجموعه‌ها سخن می‌گوییم، برای نامگذاری خود مجموعه از حروف بزرگ انگلیسی و برای معرفی عضوهای آن مجموعه از حروف کوچک انگلیسی استفاده می‌شود.

برای مثال، A یک مجموعه است، و a عضوی از A است. همین قضیه در مجموعه B با عضو b و مجموعه C با عضو c نیز صدق می‌کند.

البته این استاندارد‌ها اجباری نیستند و همچنان می‌توانید از حرفی مانند m برای نامگذاری یک مجموعه استفاده کنید، بی آنکه یک قانون ریاضیات را نقض کرده باشید؛ ولی استفاده از این نمادگذاری برای سهولت انتقال مفاهیم توصیه می‌شود.

همچنین، هنگامی که می‌گوییم عضو a در یک مجموعه A است، از علامت ∋ برای نمایش عضویت استفاده می‌کنیم. همچنین اگر عضوی در مجموعه نباشد، از علامت ∌ استفاده می‌شود.

مثال: مجموعه A برابر {3, 2, 1} است. می بینیم که 1 ∋ a، اما A ∉ 5.

تساوی

دو مجموعه زمانی با هم برابرند که تک‌تک عضوهای آنها با هم برابر باشند. ولی گاهی اوقات در نگاه اول شاید دو مجموعه برابر به نظر نرسند، پس باید دقیقا آنها را بررسی کرد.

مثال: A و B با مشخصات زیر برابرند:

• A مجموعه ای است که عضو های آن شامل 4 عدد مثبت ابتدای اعداد صحیح است و
• {B = {4, 2, 1, 3

این مجموعه‌ها را بررسی می‌کنیم. هردوی آنها شامل 1 هستند. شامل 2 هم هستند، و 3 و 4. و تمامی عضوهای طرفین را بررسی کردیم، پ نتیجه می‌گیریم که این مجموعه‌ها با هم برابرند.

و علامت مساوی ( = ) برای نمایش مساوی بودن استفاده می‌شود، پس می‌نویسیم:

A = B

زیرمجموعه‌ها

هنگامی که یک عضو را تعریف کرده‌ایم، اگر تکه‌ای از آن را برداریم، به آن تکه زیر مجموعه گفته می‌شود.

برای مثال، مجموعه {5 ,4 ,3 ,2 ,1} را در اختیار داریم. یک زیرمجموعه از این مجموعه برابر {3 ,2 ,1} است. زیرمجموعه دیگر آن {4 ,3} یا حتی {1} می تواند باشد. اما {6 ,1} یک زیرمجموعه نیست، چرا که شامل عضو (6) است که در مجموعه مادر وجود ندارد. در کل:

A یک زیرمجموعه B است، اگر و فقط اگر هر عضو A در B موجود باشد.

نکته: وقتی در ریاضیات از عبارت «اگر و فقط اگر» استفاده می‌شود، یعنی برعکس این قضیه نیز صحیح است.

این تعریف را با چند مثال بیشتر توضیح می‌دهیم:

مثال: اگر {A = {1, 3, 4 و {B = {1, 4, 3, 2، آیا A زیر مجموعه B است؟

• 1 در A هست، در B هم هست.

• 3 در A هست، در B نیز هست.

• 4 در A هست، در B هم هست.

این ها تمامی اعضای A بودند، و هر عضو آن در B وجود دارد. پس نتیجه می‌شود:

A زیرمجموعه B است.

دقت کنید که 2 در B است؛ اما در A نیست. اما به یاد داشته باشید که ایرادی ندارد، ما فقط به عضوهای زیر مجموعه نگاه می کنیم. در ادامه یک مثال سخت تر را بررسی می‌کنیم:

مثال: مجموعه A برابر تمامی مضرب‌های 4 است و B نیز تمامی مضرب‌های 2 است. آیا A یک زیر مجموعه B است؟ و آیا B زیر مجموعه A است؟

خب، در این مورد نمی‌توان تک‌تک عضوها را بررسی کرد، چون بی نهایت عضو دارد. پس ما نیاز داریم که بدانیم عضو‌های هر مجموعه به چه شکلی هستند تا ایده ای در مورد آنها داشته باشیم.

مجموعه ها برابرند با:

• {... ,A = {…, -8, -4, 0, 4, 8

• {... ,B = {…, -8, -6, -4, -2, 0, 2, 4, 6, 8

با جفت کردن عضو های دو مجموعه، می توانیم ببینیم که هر عضو A در B وجود دارد، اما هر عضو B در A وجود ندارد:

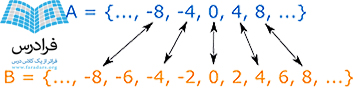
پس می‌توان نتیجه گرفت: A یک زیر مجموعه B است، اما B زیر مجموعه ای از A نیست

زیرمجموعه های محض

اگر به تعریف زیرمجموعهظ‌ها نگاه کرده و کمی فکر کنیم، نتیجه عجیبی به دست‌مان می‌آید. فرض کنید A یک مجموعه است. آیا تمامی عضوهای A در A وجود دارند؟  یعنی آیا همه اعضای یک مجموعه در خودش هستند؟ مسلم است که پاسخ این سوال مثبت است. پس این به آن معنی است که A زیر مجموعه A است.

در واقع هر مجموعه‌ای زیر مجموعه خودش است. اما شاید بخواهیم زیر مجموعه‌های یک مجموعه را به جز خودش پیدا کنیم. این زیرمجموعه‌ها، زیرمجموعه های محض نامیده می‌شوند.

A یک زیر مجموعه محض B است، اگر و فقط اگر هر عضو A در B باشد، و حداقل یک عضو در B باشد که در A نیست.

این جمله برای ما مشخص می‌کند که A زیرمجموعه محض خودش نیست. چون در غیر اینصورت یک زیرمجموعه محض کاملا با یک زیرمجموعه عادی برابر خواهد بود.

مثال:

{3 ,2 ,1} یک زیرمجموعه {3 ,2 ,1} است اما یک زیرمجموعه محض از {3 ,2 ,1} نیست.

مثال:

{3 ,2 ,1} زیرمجموعه محض مجموعه {4 ,3 ,2 ,1} است، چرا که عضو 4 در مجموعه اول وجود ندارد. دقت کنید که اگر A یک زیرمجموعه محض B باشد، پس A همچنین یک زیر مجموعه B است.

علامت‌های بیشتر

هنگامی که می‌گوییم A زیرمجموعه B است، می‌نویسیم:

A ⊆ B

یا می توانیم بگوییم که A زیر مجموعه ای از B نیست:

A ⊈ B

هنگام بحث در مورد زیر مجموعه های محض، خط زیر این علامت را بر می‌داریم و به شکل زیر در می‌آید:

A ⊂ B (زیر مجموعه محض است)

A ⊄ B (زیر مجموعه محض نیست)

مجموعه‌ی‌ تهی

این موضوع احتمالا عجیب ترین مسئله در مورد مجموعه ها است. بعنوان مثال، به مجموعه کلید های روی یک گیتار فکر کنید. اما می‌دانیم کلیدی روی گیتار وجود ندرد و تنها سیم هست. دقیقا به همین دلیل است که به مجموعه کلیدهای روی یک گیتار مجموعه‌ای بدون عضو یا تهی می‌گوییم.

هیچ عضوی در این مجموعه وجود ندارد. در واقع حتی صفر هم در این مجموعه وجود ندارد. این مجموعه با علامت ∅ یا { } (مجموعه ای بدون عضو) نشان داده می شود. یک مثال دیگر برای مجموعه تهی، مجموعه کشورهای واقع در قاره جنوبگان است.

مجموعه تهی و زیرمجموعه‌های تهی

وقتی به تعریف زیرمجموعه‌ها نگاه می‌کنیم، دیدیم که یک مجموعه به نام A تعریف کرده‌ایم. بیش از این راجع به این مجموعه توضیحی نمی‌دهیم. سوال این است که آیا مجموعه تهی زیرمجموعه‌ای از مجموعه A است؟

بر اساس تعریف، اگر تمامی عضو‌های مجموعه تهی در مجموعه A هم باشند، پس مجموعه تهی زیر‌مجموعه‌ای از A است. اما اگر هیچ عضوی وجود نداشته باشد، چطور؟

با اندکی فکر متوجه می‌شویم که این ادعا همان قدر که «بی معنی» به نظر می‌رسد، «بدیهی» نیز هست. یک راه خوب برای فکر کردن در این مورد آن است که بگوییم هیچ عضوی در مجموعه تهی وجود ندارد که در A نباشد، پس می‌فهمیم که تمامی عضوها در مجموعه تهی در A هستند. بنابراین پاسخ سوال پرسیده شده مثبت است و مجموعه تهی زیر مجموعه تمامی مجموعه ها است، حتی خود مجموعه تهی.

ترتیب

ترتیب جزو مفاهیمی است که در یک مجموعه هیچ اهمیتی ندارد. در مجموعه‌ها، عضو‌ها به هر ترتیبی که باشند، مهم نیست.

مثال: مجموعه {4 ,3 ,2 ,1} برابر است با مجموعه {2 ,4 ,1 ,3}

همان‌طوری که مجموعه‌ها متناهی و نامتناهی هستند، پس هر مجموعه‌ای شامل عضوهای محدود یا نامحدود است. برای مجموعه‌های متناهی، تعداد عضوها را با یک عدد نشان می دهیم.

مثال: {40 ,30 ,20 ,10} دارای 4 عضو است.

برای مجموعه های نامتناهی، فقط می توان گفت که عضوهای آن نامحدود است. ولی به طور کاملاً عجیبی، در مبحث مجموعه‌ها می‌توان گفت که بعضی مجموعه‌های نامتناهی از مجموعه‌های نامتناهی دیگر بزرگتر هستند؛ اما این یک بحث پیشرفته در خصوص مجموعه ها است و برای مطالعه بیشتر در این خصوص پیشنهاد می کنیم، مطالب دیگر وبلاگ فرادرس را مطالعه بکنید.